Module MM1SDM
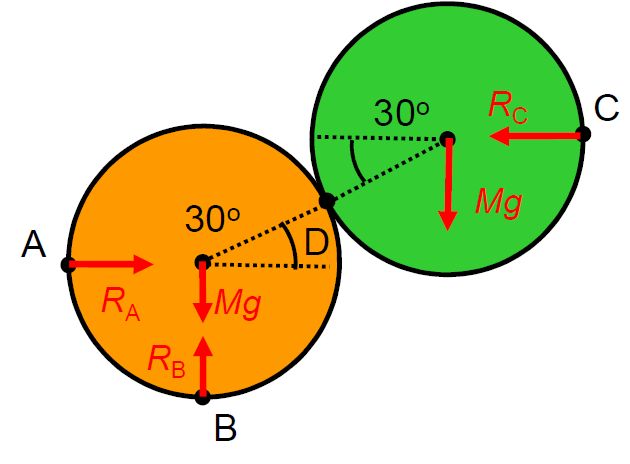
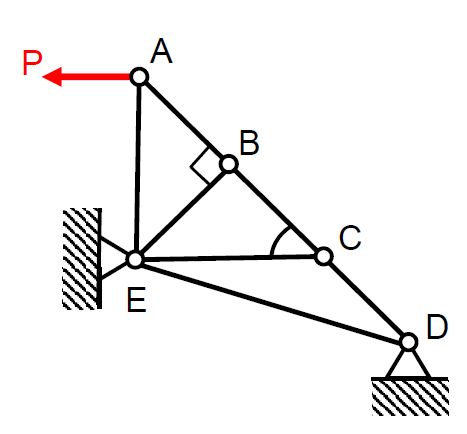
This is a core first year mechanics module covering the basics of statics and dynamics. The first semester covers statics and mechanics of solids, and is divided into three parts: the first part involves statics, such as equilibrium conditions and free body diagrams, and pin-jointed frames. Analysis is limited to 2-dimensional problems. The method of sections is taught in this part of the module.
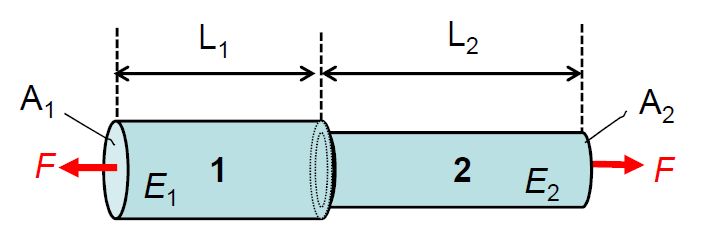
The second part is concerned with analysis of stress and strain, Mohr's circle, and torsional stresses. This is mainly concerned with 3-dimensional Hooke's law, Poisson's ratio, and uniaxial, shear and volumetric stresses and strains. Mohr's circle is taught for plane stress problems only. The torsion equation is also covered in this part, allowing computation of twist angles and shear stresses in torsion for simple sections.
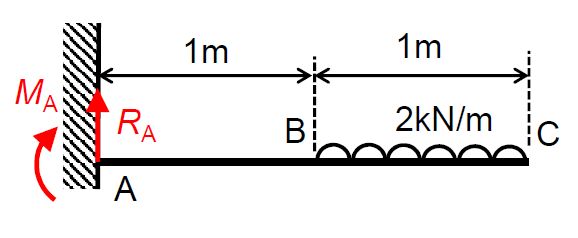
The third part involves basic analysis of bending of beams, shear and bending moment diagrams, and determination of the second moment of area for simple sections. The focus is on understanding statically determinate bending problems involving point loads, distributed loads and point moments, as well as some compound beams involving internal pins. Stresses in bending beams are also covered as part of the lectures on the neutral axis and the second moment of area.
The second semester covers dynamics, and this is taught by my colleagues Dr Samanta Piano and Dr Dimitrios Chronopoulos.
This is a fundamental module on which much of mechanical engineering is built. It requires basic A-level mathematics, and notions of mechanics and physics such as forces, moments and the concept of friction. There are two laboratories involving stress analysis of statically determinate and indeterminate beams, and bending of beams an bending stresses in the first semester, and two further laboratories involving inertia and balancing in the second semester. There is a weekly class in which students are helped with problems by me and a team of demonstrators, and approximately one lecture every three is focused on worked examples.
If you are a student enrolled on the module, you can access the course materials from Moodle by clicking here.